01好题
索引
16-17-1

16-17-1
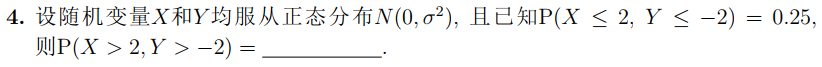
怎么分析二维正态分布呢?
16-17-1

比较的概率怎么求
要计算两个独立指数分布随机变量 和 满足 的概率,可以使用以下步骤:
1. 概率密度函数
服从均值为 1 的指数分布,其速率参数 ,PDF 为:
服从均值为 的指数分布,其速率参数 ,PDF 为:
2. 概率表达式
由于 和 独立,联合 PDF 为:
要求 ,即:
3. 积分计算
内层积分(关于 ):
外层积分(关于 ):
分解为两个积分:
计算每个积分:
第一个积分:
第二个积分:
最终结果:
4. 简化方法
对于独立的指数分布 和 ,有公式:
代入 、:
最终答案
- 目前对概率相关的运算和逻辑完全没有概念,这部分内容要总结成专题!
第一章

venn 图,找出所有的不相容种类,算出来 1156 人,超了

答案应该是错的,参考

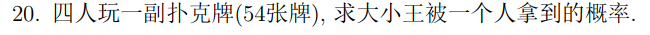 可以用高中的分隔板法。不对写你吗,54 张牌 4 个人怎么玩
可以用高中的分隔板法。不对写你吗,54 张牌 4 个人怎么玩


没做出来,答案是个确定的数字,这也太假了
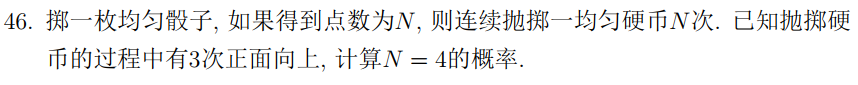
贝叶斯公式
 贝叶斯最好看的一集.
贝叶斯最好看的一集.
- 尝试理解本质,一眼看出答案
 适合更快的理解本质,这种等可能分割的情况不需要考虑分割的概率
适合更快的理解本质,这种等可能分割的情况不需要考虑分割的概率
 这更像思维题,显然第一次出正是等可能的,考虑到后续的可能性一定是乙更容易胜,所以对乙更有利。
这更像思维题,显然第一次出正是等可能的,考虑到后续的可能性一定是乙更容易胜,所以对乙更有利。
第一次等可能,1/2正面-输赢参半,1/2 反面-乙更优,合计,乙更优。