概率论第一章题目
教材上题目

样本空间和样本点定义了随机试验的模型,而事件则是对样本点的筛选

这里只考虑在同一个样本空间内的情况,即在同一个 Venn 图里

容斥原理

容斥原理
从最极端的开始,开始画 Venn 图,这个更偏向于集合论
容斥原理应满足:

建模推理
习题集
1:定义样本空间并确定指定事件的样本点(掷骰子和抛硬币实验)。
7:计算排列字母形成特定单词的概率(probability 和 ability)。
8:应用概率计算处理市场调查数据(文氏图和条件概率)。

venn 图,找出所有的不相容种类,算出来 1156 人,超了
19:计算组合场景中的概率(班级分组问题)。

答案应该是错的,参考

20:计算扑克牌分配中特定牌型的概率(大小王)。
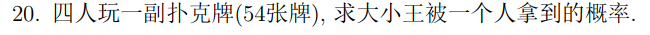
可以用高中的分隔板法。不对写你吗,54 张牌 4 个人怎么玩
21:计算抽取扑克牌包含所有花色的概率。
22:计算报纸订阅的多种概率(Venn 图应用)。

34:计算不放回抽样中的条件概率(数字 1-9)。
35:计算条件概率(数字范围内的随机抽样)。

没做出来,答案是个确定的数字,这也太假了
以上题目在 7/19 完成,有些逻辑和方法不清晰,应回顾高中概率论的常用方法
46:应用条件概率和贝叶斯公式(骰子和硬币实验)。
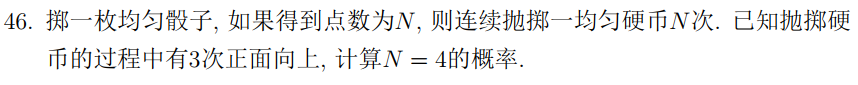
贝叶斯公式
47:解决两阶段不放回抽样概率问题(零件箱选择)。
59:计算多次独立试验的命中概率(射击实验)。ignore
69:应用贝叶斯定理比较概率(乒乓球盒子问题)。
78:分析抽样概率(白球和黑球罐子问题)。

贝叶斯最好看的一集.
- 尝试理解本质,一眼看出答案
79:使用贝叶斯定理计算条件概率(疾病诊断)。
80:不均匀硬币

86:评估概率规则的公平性(抽球游戏)。
适合更快的理解本质,这种等可能分割的情况不需要考虑分割的概率

这更像思维题,显然第一次出正是等可能的,考虑到后续的可能性一定是乙更容易胜,所以对乙更有利。
第一次等可能,1/2 正面-输赢参半,1/2 反面-乙更优,合计,乙更优。
87:分析抽奖顺序对中奖概率的影响(奖券问题)。
以上题目在 7/20 完成,应用了贝叶斯公式,掌握一些常见概率思维的应用