2_0 多维随机变量及其分布
内容来源于教材第三章,作为讲义的补充
学习目标
- 了解为什么要引入二维随机变量, 理解二维随机变量和联合分布的定义
- 理解一维随机变量和二维随机变量的差异, 掌握边缘分布和联合分布之间, 以及边缘密度函数和联合密度函数之间的联系
- 理解条件密度函数的定义, 掌握条件密度函数、边缘密度函数和联合密度函数三者之间的关系
- 掌握随机变量相互独立的定义, 并能熟练地应用独立性来求有关事件的概率
- 掌握求多个随机变量函数的分布的方法
多维随机变量及其分布
多维随机变量
有时候, 我们对随机试验的结果要用两个或两个以上的随机变量来描述, 例如为了研究某学区学龄前儿童的身体发育情况, 需要了解他 (她) 们的身高 和体重 .记 , 学龄前儿童记为 ,则 表示该儿童的身高体重. 称为二维随机变量, 它可以用来描述学龄前儿童的身体发育状况.
定义 3.1 多维随机变量
设 为同一样本空间上的随机变量, 则称
为 维随机变量, 或称为 维随机向量. 通常简记为 或
在多维随机变量中, 每个坐标都是同一样本空间中的随机变量 (图 3.1), 它们之间还会有某种关系, 所以研究单个随机变量是不够的. 我们必须把它们放在一起进行研究.
先研究二维随机变量. 类似于一维随机变量, 我们也是要研究它们取哪些值以及取这些值的概率多大. 这就引入如下定义:
定义 3.2 二维分布函数
设 是二维随机变量, ,称二元函数
为 的分布函数, 或 的联合分布函数 (joint cdf).
由二维联合分布函数 ,我们可以求出二维随机向量 落在矩形区域 中的概率
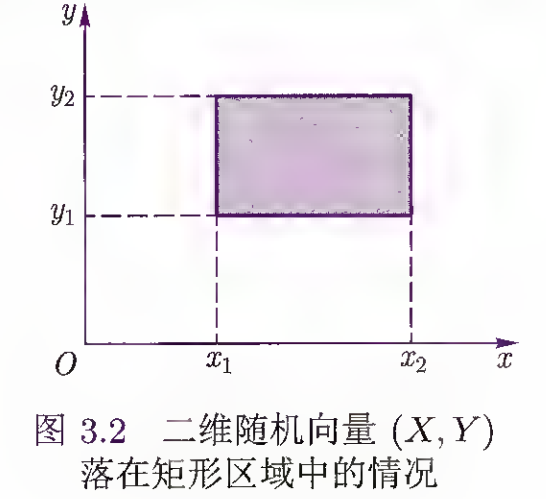
性质 - 二维联合分布函数
二维随机变量的联合分布函数 具有如下性质:
(1) 分别对 单调不减的:
(2)
(3) 分别关于 右连续;
(4) 非负, 即
这 4 条性质的证明容易, 它们刻画了一个二维联合分布函数, 即一个二元实函数 如果满足上述 4 条性质, 那么必存在随机变量 和 , 使得 为它们的联合分布函数. 值得注意的是, 二维随机变量与一维随机变量不同, 刻画一个联合分布函数需要加上 (4). 也就是说从条件 (1)~(3) 推不出 (4).
例 3.1 定义二元函数
则 满足上述性质中的 (1)~(3), 但不满足 (4), 因而不是一个分布函数.
证 性质 (1)~(3) 容易验证. 对 (4), 因为
从而得证. 事实上, 我们容易找到无穷多个不满足性质 (4) 的矩形.
当然, 对于二维离散型随机变量, 即每个分量都是离散型的随机变量, 我们不必用联合分布函数来描述其概率分布情况, 而可以指出它们在每个可能的取值点上的概率值即可.
定义 3.3 二维离散型随机变量
设 的可能取值为 . 记
称其为二维离散型随机变量的联合概率质量函数或联合分布律 (joint pmf).
容易验证
(1) ;
(2) .
当 都取有限个值时, 也常用下面的列表表示它们的联合分布律:
一般地, 对 维离散型随机变量, 我们有下述定义:
定义 3.4 维离散型随机变量
称 为 维离散型随机变量, 若每一个 都是一个离散型随机变量, .并设 的所有可能取值 (有限个或可数个) 为 ,则称
为 维随机变量 的联合概率质量函数或联合分布律。
容易证明联合分布律具有下列性质:
(1)
(2)
例 3.2 期末有高等数学和普通物理两门课程的考试, 高等数学先考. 对某些同学而言, 第一门课程的成绩对第二门课程成绩有影响. 设某学生高等数学考试优秀的概率为 0.6, 若高等数学成绩优秀, 则他的普通物理考试优秀的概率为 0.8, 反之, 若他的高等数学成绩良好或以下, 则物理考试成绩为良好或以下的概率为 0.7. 求该学生两门课程考试得分概率的所有情况.
解令 .其中 高等数学考试成绩优秀 普通物理考试成绩优秀}. 题意就是求 的联合分布.
列表表示如下:
| X | Y | |
| 0 | 1 | |
| 0 | 0.28 | 0.12 |
| 1 | 0.12 | 0.48 |
例 3.3 (多项分布) 设 为某一试验下的完备事件群, 即 两两不相容且和为 .记 ,则 现将试验独立重复进行 次, 分别用 表示事件 出现的次数 .则 为一离散型随机变量, 试求 的分布函数. 此分布律称为多项分布, 记为
解 由于试验独立进行, 总的结果数为 , 记结果 出现的次数为 , 则 . 因此相当于多组组合, 所以
其中 为非负整数且 .
连续型多维随机变量的联合密度函数
回想我们定义一元连续型随机变量的思路, 对随机变量在 上任意 (可测) 区间的概率, 通过寻找其概率密度函数这一本质工具, 从而可以将其表示为概率密度函数在该区间上的积分. 由于多维欧式空间和直线有着相似的优良性质, 一元连续型随机变量的定义可以自然地推广到二维和多维场合, 我们首先看二维连续型随机变量的定义:
定义 3.5 二维连续型随机变量
设 , 若存在可积的非负函数 , 使得对于 , 有
则称 为二维连续型随机变量, 称为其联合分布函数, 称 为其联合概率密度函数 (joint pdf), 简称联合密度函数.
性质 - 联合概率密度函数
具有以下性质: (1) 对任意的 , 有
(2)
(3) 若 在点 处连续, 则
由此知
即 大约是二维随机变量落在矩形 中的概率.
(4) 设 是平面上的一个区域, 则
- 这里有个问题没有解决,那就是条件概率的情形,其中一个概率是固定的,如 概率论第三章题目 中的第 23 题
可以从质量来理解二维联合概率密度函数和联合分布函数, 可以解释为面密度, 该公式解释为该区域的质量. 从几何角度看, 上面的公式是平面区域 上方和曲面 之间的柱形体积.
Tip
从定义可以看出, 连续型随机向量与离散型随机向量不同, 不能简单地定义为 " 每个分量都是一维连续型随机变量 “. 即使随机向量的每个分量都是连续型随机变量,它们的联合分布也不一定存在联合概率密度函数
例 3.4 设 , ,则随机向量 的两个分量都是连续型随机变量, 但 只能在单位正方形的对角线取非 0 值, 因而不可能存在一个非负函数 满足性质 (2)(因为二元黎曼可积函数在平面上任一有限线段上的积分为 0), 即 不存在密度函数. 3 均匀分布
性质 (4) 中的区域 通常用 的若干个函数不等式来表示, 大多数情况下为由 的线性函数和二次函数围成的.
例 3.5 设 的概率密度函数为
其中 , , 称 服从参数为 的二元正态分布, 记为 .图形参考
例 3.6 设 是平面上的一个有界区域, 记 为 的面积, 若
称 在 上服从均匀分布.
例 3.7 设
设区域 G 由
围成 (见图 3.4). 求 及
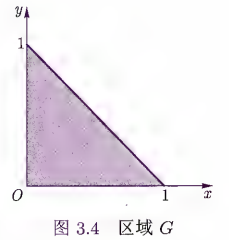
解 联合分布函数为
注 二维随机变量的联合分布函数和联合概率密度函数可以毫无困难地推广到 维. 设 , , 称
为 维随机变量 的联合分布函数. 若存在非负的 元函数 , 使得
则 称为 的联合密度函数, 称为连续型的 维随机变量, 对应的联合分布函数 称为连续型的联合分布函数.
可以验证联合分布函数 具有下述性质:
(1) 对每个变元单调不减;
(2) 对任意的 有, ;
边缘 (际) 分布
多维随机向量的每个分量或子集均为随机变量,那么它们的分布函数可以从联合分布函数导出。我们称这些分量或子集的分布函数为边缘(际)分布函数,以强调它们可以从联合分布函数中导出来。
定义 3.6 边缘(际)分布
设 的联合分布函数为 ,则其分量 和 的分布函数 和 称为 或 的边缘(际)分布 (marginal distribution).
视频扫描视频 9 的二维码观看关于边缘分布和条件分布的讲解
由于 ,故
同理,
由此知联合分布可以唯一确定边缘分布. 下面分别对二维离散型和二维连续型随机变量的边缘分布进行讨论.
二维离散型随机变量的边缘(际)分布
设二维离散型随机变量 的联合分布律为
则随机变量 的边际分布律为
同理,随机变量 的边缘分布律为
在例 3.2 中,由联合分布律容易得到 的边缘分布律为
以及 的边缘分布律为
用列表表示更清楚:
| X | Y | pi. | |
| 0 | 1 | ||
| 0 | 0.28 | 0.12 | 0.4 |
| 1 | 0.12 | 0.48 | 0.6 |
| p.j | 0.4 | 0.6 | 1 |
例 3.8 袋中有 5 张外形相同的卡片, 3 张写上数字 ,另 2 张写上数字 .现从袋中任取两张卡片, 分别以 表示第一张和第二张卡片上的数字, 试求分别在有放回和不放回两种情形下, 的联合分布律及 的边缘分布律.
解简单计算得到
| Y | X | p.j | |
| 0 | 1 | ||
| 0 | 9 | 6 | 3 |
| 25 | 25 | 5 | |
| 1 | 6 | 4 | 2 |
| 25 | 25 | 5 | |
| pi. | 3 | 2 | 1 |
| 5 | 5 | ||
| Y | X | p.j | |
| 0 | 1 | ||
| 0 | 6 | 6 | 3 |
| 20 | 20 | 5 | |
| 1 | 6 | 2 | 2 |
| 20 | 20 | 5 | |
| pi. | 3 | 2 | 1 |
| 5 | 5 | ||
这个例子说明, 边缘分布律不能决定联合分布律. 其中, 左边表为有放回抽取下的分布律, 右边表为不放回抽取下的分布律. 口
二维连续型随机变量的边缘分布
设二维连续型随机变量 ,由于
右边在积分号下对 求导, 得 的边缘概率密度函数为
同理, 的边缘概率密度函数为
定义 3.7 边缘概率密度函数
和 的概率密度函数 和 称为二维随机变量 或者联合概率密度函数 的边缘概率密度函数 (marginal pdf), 简称边缘密度函数.
由定义不难看出, 计算二维连续型随机变量的边缘密度函数就是联合密度函数 对
另一个变量求积分.
例 3.9 (例 3.5 续) 二元正态分布的联合概率密度函数 可以表示为下述形式 (表示为 元正态分布密度函数的一般形式): 如果 ,其中概率密度函数为
其中 为常数列向量, 为正定方阵, 为 的行列式,
其中 求 和
解不难得到
要得到 的边缘概率密度函数, 只要在联合概率密度函数 中对 积分. 作变量代换
对 积分, 注意到标准正态分布密度函数 的积分为 1, 得
同理,
可以看到, 随机变量 都服从正态分布, 但是它们都与参数 无关, 这说明联合分布可以唯一确定边缘分布, 但是两个边缘分布不能唯一确定联合分布. 口
例 3.10 设随机变量 有如下的联合概率密度函数:
则不难验证, 它的两个边缘概率密度函数都是正态分布密度函数.
解 事实上, 在例 3.9 中, 取 , 则容易得到
本例也说明边缘概率密度函数不能决定联合概率密度函数.
例 3.11 考虑两个概率密度函数
试求边缘概率密度.
解 易得所求边缘概率密度都是如下形式:
这说明边缘概率密度函数不能决定联合概率密度函数.
注 多维随机变量的边缘分布和边缘密度函数
(1) 边缘分布的概念可以推广到多维随机变量, 其中仅仅是把随机变量换成随机向量. 设 , 从这 个随机变量中任取 个 , 记 , 为方便起见, 不妨设 , 剩下的 个随机变量记为 , 则 的分布就称为 维随机变量 的边缘分布, 记为 , 其中 , 注意到
即在联合分布函数中, 把另一个变量用 代替就得到边缘分布.
(2) 类似于讨论二元随机变量的边缘密度函数, 边缘密度函数等于联合密度函数对另一个变量的积分. 用随机向量 代替二元函数中的 , 得到多维随机向量的边缘密度函数等于联合密度函数对另一个变量 的积分, 其中 , 即
其中 .
(3) 维随机变量的边缘分布函数有 个.
条件分布
一个随机变量 (或向量) 的条件概率分布, 就是在给定 (或已知) 某种条件 (某种信息) 下该随机变量 (向量) 的概率分布.
当 为二维离散型随机变量时, 设联合分布律为
若 , 则根据条件概率的定义, 在给定 下 的条件分布律为
同理若 , 则给定 下 的条件分布律为
当 为二维连续型随机变量时, 记联合概率密度函数为 . 由于连续型随机变量取任意一点的概率为 0, 故此时不能直接使用条件概率. 但是注意到, 如果定义条件分布函数
其中 的概率密度函数在 处的值 (显然, 在固定 时是一个分布函数). 根据连续型随机变量的定义和概率密度函数的性质, 上式定义了 在给定条件 下的分布函数和概率密度函数. 也就是说, 条件分布函数 可以表示为非负函数 的积分, 故其为概率密度函数, 则定义
定义 3.8 条件概率密度函数
如果 的概率密度函数在 处的值 , 那么称
为给定 下随机变量 的条件概率密度函数 (conditional pdf), 简称条件密度函数. 同理, 给定 下随机变量 的条件概率密度函数 为
给定 下随机变量 的条件密度函数也常常表为 , 或 .
由条件密度函数的定义, 我们有
由此得到连续型随机变量的贝叶斯公式的密度函数形式:
注 (条件分布的物理直观意义) 从物理观点看, 设平面上在格点 上有质量 就是直线 的质量. 就是格点 上质量与直线 质量的比值. 如果平面质量有面密度 , 就是当 时矩形 与条形 质量比值的极限. 而条件分布函数 就是当 时, 条形 与条形 质量比值的极限.
例 3.12 从 (0,1) 中任取一点 , 再从 中任取一点 , 求 的密度函数以及 .
解 由题意, , , 所以由公式 (3.10), 的联合密度为
当 时,
由条件密度函数定义知
因此
例 3.13 设某地区成年男子的身高 服从正态分布 , 当身高 时, 体重 (单位: ) 服从正态分布 . 求体重 的分布.
解 由题意,
所以
在 的指数中, 对变量 配平方, 然后对 积分, 得
即
例 3.14 设 ,求 的分布.
解 由二元正态分布随机变量密度函数的定义, ,密度函数记为 ,记
则
即
注 ( 维随机变量的条件密度函数) 把随机变量 都换成随机向量 ,我们可以把两个随机变量的条件密度函数推广到 维随机变量的条件密度函数. 设
记随机向量 的边缘密度函数分别为 和 ,则给定随机向量 下随机
向量 的条件密度 定义为
同理, 给定随机向量 下随机向量 的条件密度 定义为
类似于二维随机变量的贝叶斯公式的密度函数形式, 对 维随机变量也成立.
相互独立的随机变量
在上一小节中, 我们知道由 的联合分布可以唯一确定边缘分布, 反之不必成立. 什么时候边缘分布可以唯一确定联合分布? 在研究事件独立性时, 我们知道两个事件同时发生的概率等于每个事件发生概率乘积的充要条件是这两个事件相互独立. 的联合分布
也是两个事件同时发生的概率, 要上式等于 和 的乘积, 就需要事件 和 相互独立. 不过由于 可以在平面上变化, 所以这不是两个事件了. 为此我们需要引入随机变量相互独立的概念.
定义 3.9 随机变量相互独立
设随机变量 的联合分布为 , 边缘分布为 . 若 , 都有
则称随机变量 相互独立.
视频扫描视频 10 的二维码观看关于随机变量的独立性的讲解
直观来看, 称随机变量 相互独立是指: 若 是与随机变量 相关的任意事件, 是与随机变量 相关的任意事件, 则事件 相互独立. 所以随机变量独立的定义也等价于: , 都有
若 是离散型随机变量, 分布律为 , 则 相互独立等价于
事实上, 充分性显然, 下证必要性. 因为 相互独立, 所以有
因此, 对任意的取值对 , 有
从而得证.
若 是连续型随机变量, 有联合概率密度函数 和边缘概率密度函数 ,则不难证明 相互独立等价于
上式等价于密度函数 可以分离变量, 即若有
其中 不必是概率密度函数
在实际问题中, 随机变量的独立性是可以知道的, 如在掷骰子的游戏中, 令 第 次掷出的点数 .则第 2 次掷得点数与第 1 次掷得点数没有任何关系, 是相互独立的. 在购买彩票中, 这次开出什么号码与下次开出什么号码没有任何关系, 也是独立的. 我们可以利用随机变量的独立性来计算有关随机事件发生的概率.
例 3.15 (会面问题) 两人约定上午 在公园东大门会面, 先到者等候 , 如果另一人还没到就可以离开. 求两人能会面的概率.
解设 分别表示两人到达的时间, 由题意, 且 相互独立. 两人能会面: (图 3.5). 所以两人能会面的概率为

图 3.5 会面问题
例 3.16 (不独立的随机变量) 设 的联合密度函数为
求证 不相互独立.
证 用反证法, 若 相互独立, 则 , 有 . 如图 3.6, 在单位圆和外接正方形之间任取一点 , 则 , 而
同理, , 所以在该点 , 矛盾. 因为单位圆和外接正方形之间的面积大于 0, 所以 不相互独立.
例 3.17 (两个正态分布随机变量独立的充要条件) 设 , 证明: 相互独立
证充分性. 若 , 因为 , 即联合密度函数可分离, 所以 相互独立.

图 3.6 单位圆和外接正方形
必要性. 若 相互独立, 则 , 特别取 , 有
从而
两个随机变量相互独立可以推广到 个随机变量相互独立
定义 3.10 多维随机向量的相互独立性
设 维随机变量 , 记 , . 若对任意 都成立
则称随机变量 相互独立.
性质利用分布函数与分布律或概率密度函数之间的关系, 容易得到
(1) 若随机向量 是 维离散型随机向量, 若对所有可能取值 都成立
则称随机变量 相互独立.
(2) 设连续型随机向量 , , , 若对任意 都成立
则称随机变量 相互独立.
(3) 若 个随机变量 相互独立, 则随机向量 和随机向量 相互独立. 当然, 随机向量的函数 和 也是相互独立的.
然而一般来说, 仅由某一部分独立无法推出 相互独立. 见下例.
例 3.18 若 相互独立, 都服从 和 1 这两点上的等可能分布. ,证明: 两两独立但不相互独立.
证 由题设知 均服从 和 1 这两点上的等可能分布, 注意到
因此, 与 相互独立. 类似可证 与 相互独立. 即 两两独立. 但是
即 不相互独立. 从而得证.
随机向量函数的分布
我们已经知道若随机变量 是随机变量 的函数时, 的分布可以由 的分布表达. 把随机变量 推广到随机向量时, 也有相应的表达. 我们仅仅讨论二维连续型随机向量的函数, 离散情况和多维情况没有实质性的区别, 仅仅是表达式复杂点.
设 , 为一维随机变量, ,则
特别当 时, 的分布函数 为
若 分别为一维随机变量, , 则 的联合分布为
特别当 时, 的联合分布函数 为
有了分布函数, 对它求导即可得密度函数. 为计算 (3.21) 式, 有时要用到二元函数的变换. 令 和 一一对应. 反函数记为 且都有一阶连续偏导数, 记 对 和 对 的雅可比 (Jacobi) 行列式分别为
注意到
则作变换后
在 (3.23) 式中对 求混合偏导, 得
特别地, 当随机变量 相互独立时, 有 , 计算会方便进行.
视频扫描视频 11 的二维码观看关于两个随机变量的函数的分布讲解.
在多维随机变量场合, 更一般地有, 如果 是 维连续型随机向量, 具有联合概率密度函数 .假设存在 到 的一一映射 ,其逆映射 存在一阶连续偏导数, 那么 维随机变量 是连续型的, 且具有联合密度函数
其中 是随机向量 的密度非零的所有可能值的集合, 是变换的雅可比行列式, 这里 为行列式 的绝对值, 即
例 3.19 设随机变量 相互独立, 分别具有概率密度函数 和 , 求 的概率密度函数.
解 由 相互独立及公式 (3.20)
在积分号下对 求导, 得
这里 称为 和 的卷积 (convolution).
也可以从变量代换角度来得到随机变量和的密度函数. 令 , 函数 对 的雅可比行列式为 1, 故 (积分区域如图 3.7)

图 3.7 积分区域
由密度函数的定义
当 相互独立时, . 这里不需要在积分号下求导.
例 3.20 (指数分布随机变量的和与差) 设 和 独立, 均服从指数分布 ,求 的概率密度函数.
解 由于
进一步容易得出, 如果 相互独立且服从相同的指数分布 ,那么 的概率密度函数为
该分布称为参数是 的 分布, 记为 . 如果相互独立的两个同类型随机变量之和仍服从同一类型的分布, 那么称此分布类型具有再生性. 因此, 分布对参数 具有再生性.
类似地, 的概率密度函数为
该分布称为拉普拉斯分布, 即独立指数分布的差是拉普拉斯分布.
例 3.21 设 相互独立, 且 , 求 的概率密度函数.
解令 , 由于 , 故 的联合密度函数为
(联合密度函数的非零区域见图 3.8), 对另一个变量求积分得到 的密度函数为

例 3.22 (正态分布随机变量的和)设 和 相互独立, 分别服从 和 ,求 的分布.
解由于
即 ,即正态分布 对参数 具有再生性.
值得注意的是,这里“ 和 相互独立”这一条件不能少.事实上,容易验证(读者练习.)
为一个二元概率密度函数, 且满足 和 的边缘分布均为标准正态分布, 但是 的分布不是正态分布.
例 3.23 (独立随机变量商的分布) 设 和 相互独立, ,求 的分布.
解令 ,则当 时, 函数 对 的雅可比行列式的绝对值为
所以 对 的雅可比行列式的绝对值为 ,由此得
由密度函数的定义知
例如, 设 和 是独立的随机变量, 均服从 。则
该分布称为柯西 (Cauchy) 分布, 即独立正态分布随机变量的商服从柯西分布。
例 3.24 设 和 相互独立, ,求 的极坐标变换后极轴和极角 的分布。
解由定义, 作极坐标变换 ,其中 。则 对 的雅可比行列式的绝对值为 ,由于
作极坐标变换后由 (3.24) 式得
由上式知, 极坐标变换后的 是相互独立的。其中 。
例 3.25 设随机变量 相互独立且都服从区间 上的均匀分布。
(1) 若随机变量 ,其中 为一给定常数, 试求 的概率密度函数。
(2) 试求随机变量 的分布函数。
(3) 试求随机变量 的概率密度函数。
解 (1) 对任意 , 由于
故 服从参数为 的指数分布, 从而其概率密度函数为 .
(2) 当 时,
而当 时,
故 的分布函数为
(3) 由 及
(1) 可知, 为 3 个独立的服从 的随机变量之和, 故 服从 分布, 即其概率密度函数为
再由 及密度函数变换公式可知, 的概率密度函数为
例 3.26 (最大值和最小值的分布) 设 和 相互独立, , 求 和 的分布.
解 首先注意 和 均为随机变量. 由于 和 相互独立, 故
如果 , 那么
此例可以毫无困难地推广到 个相互独立随机变量的最大值和最小值的分布.
例 3.27 掷两颗骰子, 设 和 分别表示第一和第二次掷出的点数, 求 和 .
解注意到 和 相互独立, 有
例 3.28 (系统可靠性研究) 设系统 由两个独立的子系统 连接而成, 连接的方式分别为 (1) 串联, (2) 并联, (3) 备用, 如图 3.9. 设 的寿命分别为 ,其密度函数分别为
其中 .求系统 的寿命 的分布

图 3.9 系统连接方式
解 (1) 串联, 只要 中有一个损坏, 系统 停止工作, 故 ,由 (3.27) 式得
(2) 并联, 只有 两个都损坏时, 系统 才停止工作, 故 ,由 (3.26) 式得
(3) 备用, 系统 和 寿命之和. 即 ,故 时, 由独立随机变量密度函
数卷积公式,
若 ,容易得到
扩展阅读:辛普森情论
有人说统计会撒谎. “世界上有三种谎言, 即谎言、弥天大谎和统计 (There are three kinds of lies: lies, damned lies and statistics)”. 美国作家马克·吐温 (Mark Twain, 1835—1910) 在其作品《我的自传》中的曾引用此话. 将统计和谎言相提并论显然有失公允. 如今人们理解这句话, 大多指向的是对统计数据的人为操纵和恶意利用. 其实, 数字本身不会说谎, 数字只是一个信息载体, 说谎的其实是使用数字的人. 数字既可以拿来解释客观世界, 也可以用来曲解事实真相. 这也恰好说明, 如果没有一定的统计学知识, 人们就有可能从接收到的信息里得出错误的结论. 美国统计学家哈夫 (Darrell Huff, 1913—2001) 还为此出版了一本名为《统计数字会撒谎》(How to Lie with Statistics) 的科普读本. 该书用大量生动有趣的实例, 揭露了当时美国社会中一些利用数字和数据造假的现象, 引起了极大反响. 书中提出的统计陷阱的例子, 比如样本选择偏差、平均数的选择以及相关性的滥用等, 在现今的生活中仍然十分常见. 该书自 1954 年出版至今, 多次重印, 被译为多种文字, 影响深远, 光在国内出版的中译名就有《统计陷阱》《统计数字会撒谎》《怎能利用统计撒谎》和《别让统计数字骗了你》等. 在日常的经济生活中, 我们将接触到越来越多的统计数据和资料, 例如各种证券信息、投资可行性研究报告、公司财务报告等, 这些资料和数据如何去伪存真, 如何进行鉴别? 没有很好的统计思维, 就很有可能陷入那些精心炮制的数据陷阱之中, 从而得出有失偏颇的结论.
下面我们将通过统计学里一个有名的辛普森情论来说明统计是如何“撒谎”的.
什么是辛普森情论
当人们尝试探究两种变量是否具有相关性的时候, 比如新生录取率与性别, 报酬与性别等, 会分别对之进行分组研究. 辛普森悖论是在这种研究中, 在某些前提下有时会产生的一种现象, 即在分组比较中都占优势的一方, 在总评中反而会是失势的一方. 该现象于 20 世纪初就有人讨论, 但一直到 1951 年英国统计学家辛普森 (Edward H. Simpson, 1922— ) 在他发表的论文中该现象才算正式被描述和解释. 后来就以他的名字命名该悖论.
我们通过一个虚构的简单例子来说明什么是辛普森悖论. 一所高校的两个学院, 分别是法学院和商学院. 人们怀疑这两个学院在新生招生中有性别歧视.
如表 3.1 所示, 无论在法学院还是在商学院, 女生的录取比例都高于男生, 由此可以推断
学校在招生时更倾向于招女生吗?但是,如果将两个学院的数据汇总,结果如表 3.2 所示,却发现女生的总体录取率实际上比男生要低.
表 3.1 各学院录取率
| 法学院男生 | 法学院女生 | 商学院男生 | 商学院女生 | |
| 录取人数 | 8 | 51 | 201 | 92 |
| 未录取人数 | 45 | 101 | 50 | 9 |
| 录取率/% | 15.1 | 33.6 | 80.1 | 91.1 |
表 3.2 总体录取率
| 男生 | 女生 | |
| 录取人数 | 209 | 143 |
| 未录取人数 | 95 | 110 |
| 录取率/% | 68.8 | 56.5 |
上面的例子说明简单地将分组数据相加汇总有时并不能反映真实的整体情况.这种看起来“自相矛盾”的情况是怎么发生的呢?就这个例子来说,导致辛普森论发生一般有两个前提.
第一,两个分组的录取率相差很大,即法学院录取率很低,而商学院却很高.另一方面,两种性别的申请者分布比率相反,即法学院大部分申请者为女性,而商学院大部分申请者为男性.结果在数量上来说,拒收率高的法学院拒收了很多的女生,男生虽然有更高的拒收率,但被拒收的数量却相对不算多.而录取率很高的商学院虽然有较高的录取比例,但是被拒收的男生数量相对法学院来说则明显较多.
第二,有潜在因素影响着录取情况,即性别并非是影响录取率高低的唯一因素,甚至可能是毫无影响的.至于在学院中出现的比率差,可能只是随机因素造成的,又或者是其他因素作用 (如入学成绩). 刚好出现这种录取比例,使人牵强地误认为这是由性别差异而造成的.
辛普森论也可以从数学上解释,即若有
但并不能保证
这个结论很初等,我们相信很多同学能给出适当的例子以验证,只是对很多人来说比较“反常识”而已.
辛普森论的重要性在于它揭示了:我们看到的数据并非全貌.我们不能满足于展示的数字或图表,需要考虑整个数据生成过程,将所有可能的因素或变量考虑进来以通过它们的联合分布来研究.一种更深刻的解释是统计学中的因果推断.一旦我们理解了数据产生的机制,
我们就能从图表之外的角度来考虑问题, 找到其他影响因素. 如果两个统计变量 与 之间存在因果关系, 那么这种因果关系存在三个可能, 要么是 导致 , 要么是 导致 , 或者存在一个共同的原因 , 同时导致了 与 .
本章总结

图 3.10 第三章知识点结构图
重点概念总结
取有限个值的二维离散型随机变量的分布律一般用矩形表格来表示, 由此可以方便获得边缘分布和条件分布.
如果 服从二元正态分布, 那么唯一确定的两个边缘分布都是正态分布, 反之, 边缘分布不能唯一确定联合分布.
计算有关事件概率的难点是计算二重积分, 计算二维随机变量的函数分布的关键之一是二重积分中的变量代换.
为了求出 的密度函数, 可以令 , 先求出 的联合密度函数, 然后对其中一个变量积分获得另一个变量的密度函数.
利用条件密度函数、边缘密度函数和联合密度函数三者之间的关系计算联合密度函数或边缘密度函数.
两个随机变量相互独立是指: 任取与 有关的事件 以及与 有关的事件 , 则事件 相互独立, 由此来理解随机变量独立的定义以及计算有关的概率.
习题
-
箱中装有 6 个球, 其中红、白、黑球的个数分别为 1,2,3. 现从箱中随机地取出 2 个球, 记 为取出的红球个数, 为取出的白球个数. 求随机变量 的联合分布函数.
-
袋中有一个红球, 两个黑球, 三个白球, 现有放回地从袋中取两次, 每次取一球, 以 , 分别表示两次取球的红、黑、白球的个数.
(1) 求 ;
(2) 求二维随机变量 的联合分布函数.
-
将同一硬币连续掷三次, 以 表示在三次中出现正面的次数, 以 表示三次中出现的正面次数和出现的反面次数之差的绝对值. 试写出 和 的联合分布律.
-
现有某种产品 100 个, 其中一、二、三等品分别为 80,10,10 个, 现从中随机抽取一个产品, 记
求 的联合分布律
-
设二维随机向量的联合分布律为
| Y | X | |
| -1 | 1 | |
| -1 | 0.2 | b |
| 1 | a | 0.3 |
已知事件 和 相互独立, 求
- 设某射手每次射中目标的概率为 , 射击进行到第二次射中目标为止, 表示第一次射中目标所进行的射击次数, 表示第二次射中目标所进行的射击次数.
(1) 求二维随机变量 的联合分布律;
(2) 求 和 的边缘分布.
-
从 1,2,3,4 四个数中任取一个数, 记为 , 再从 1 到 中任取一个数, 记为 , 求事件 发生的概率.
-
设二维随机变量 服从正态分布 , 求 .
-
设二维随机变量 的联合分布函数为
(1) 确定常数
(2) 求 ;
(3) 求 和 的边缘密度函数.
- 设二维随机变量 的密度函数为 (1) 试求 的分布函数;
(2) 试求概率
- 设二维随机变量 的密度函数为 (1) 求条件密度函数
(2) 求条件概率
-
设二维随机变量 的密度函数为
求常数 及条件密度函数
-
设二维随机变量 的密度函数为
求常数 及条件概率
-
设随机变量 与 相互独立, 且 服从标准正态分布 , 的分布律为 , 求随机变量 的分布函数.
-
设 和 是相互独立的随机变量, , , 其中 为常数. 引入随机变量
求 的分布律.
-
设二维随机变量 的密度函数为
(1) 求 的值;
(2) 求 落在圆 内的概率.
- 设 是二维随机变量, 的边缘密度函数为 在给定 的条件下, 的条件密度函数为 (1) 求 的联合密度函数
(2) 求 的边缘密度函数
- 设随机变量 的密度函数为 , 而随机变量 服从 上的均匀分布, 求
(1) 的联合分布函数;
(2) 随机变量 的分布函数.
-
设在 的条件下, 服从参数为 的泊松分布, 已知 服从参数为 1 的指数分布, 求 的分布律.
-
设 是矩形 上的均匀分布, 求随机变量 的密度函数.
-
设 在区域 上服从均匀分布, 由 与 围成. 试求
(1) 边缘密度函数
(2) 条件密度函数
- 设随机向量 服从区域 内的均匀分布, 其中 是由直线 所围成的区域, 试求
(1) 的联合密度函数
(2) 的边缘密度函数 和
(3) 条件密度函数
(4)
-
设 服从矩形 内的均匀分布, 记
求 的联合分布函数.
-
从一副扑克牌 (共 52 张) 中任取 13 张, 以 和 分别记其中的黑桃和红桃张数. 试求:
(1) 的联合概率质量函数;
(2) 已知取出的只有一张黑桃, 求此时 的条件概率分布.
- 假设有 个不同的盒子与 个相同的小球,每个小球独立地以概率 落入第 个盒子 .分别以 表示落入各个盒子的球数. 试求
(1) 的联合分布函数;(2) 的边缘分布函数,其中
(3) 的边缘分布函数;(4) 在 的条件下, 的条件分布函数.
- 设随机变量 与 相互独立, 的概率分布为 的密度函数为 记
(1) 求
(2) 求 的密度函数.
29, 34, 35, 40, 43
-
设随机变量 与 相互独立, 服从参数为 1 的指数分布, 服从标准正态分布,求 的联合密度函数.
-
设某班车起点站上客人数 服从参数为 的泊松分布,每位乘客在中途下车的概率为 ,且中途下车与否相互独立,以 表示中途下车的人数,求
(1) 在发车时,有 个乘客的条件下,中途有 个人下车的概率;(2) 二维随机变量 的概率分布.
-
设 ,且随机变量 相互独立. 求 的分布.
-
设 是两个相互独立的随机变量, 在 上服从均匀分布, 的密度函数为
(1) 求 的联合密度函数;(2) 求二次方程 有实根的概率.
-
设 服从单位球 内的均匀分布,试求 的边缘分布.
-
设随机变量 的分布律分别为
| X | 0 | 1 |
| P | 1/2 | 1/2 |
| Y | -1 | 0 | 1 |
| P | 1/4 | 1/2 | 1/4 |
且
(1) 求 的联合分布;(2) 问 是否独立.
- 连续地掷一颗均匀的骰子,直到出现点数大于 2 为止,以 表示掷骰子的次数,以 表示最后一次掷出的点数.
(1) 求二维随机变量 的联合分布以及 的边缘分布;(2) 问 和 是否相互独立.
-
令 和 为独立的离散型随机变量,且在 上均匀分布,考虑
研究 的独立性和两两独立性
-
设 的联合密度函数为
(1) 求系数
(2) 与 是否独立;(3) 求 的密度函数
(4) 试求
- 设随机向量 服从 内的均匀分布,
(1) 试求出 和 的边缘分布;(2) 和 是否相互独立?(3) 求在 时, 的条件密度函数.
-
设 的联合密度函数为
(1) 求给定 时, 的条件密度函数;(2) 证明 和 相互独立.
-
设随机变量 的分布律分别为
| X | 0 | 1 |
| P | 1/3 | 2/3 |
| Y | -1 | 0 | 1 |
| P | 1/3 | 1/3 | 1/3 |
且 .求
(1) 的联合分布;(2) 的概率分布.
- 设 服从正方形 内的均匀分布,
(1) 求 与 的边缘分布;(2) 问 是否相互独立?
-
设随机向量 的密度函数为
(1) 求 与 的边缘密度函数;(2) 问 与 是否相互独立?(3) 计算
-
设 的联合分布函数为
(1) 求 的边缘分布函数 和
(2) 求 的联合密度函数 以及边缘密度函数
(3) 验证 是否相互独立.
-
设随机向量 的联合密度函数为
证明: 两两独立但不相互独立
-
设随机向量 的密度函数为
证明: 不独立但是 是相互独立的
-
设连续型随机变量 为取有限值的离散型随机变量,且 相互独立.
(1) 求 的分布. 由此回答随机变量 是否为连续型的?(2) 求 的分布,问 是不是连续型随机变量?以 为例求出 具体的分布.
-
在长度为 1 的线段上任取两点,把线段分为 3 段,求这 3 条线段能组成三角形的概率.
-
- 设随机变量 的密度函数为 , 令 (1) 求随机变量 的分布函数;
(2) 随机变量 的分布有什么特点?
-
- 设 , 证明: 存在常数 , 使 相互独立.
-
- 设 , 证明
(1) 随机变量 与随机变量 相互独立;
(2) 利用 (1) 的结论证明
49. * (多项分布) 设 是样本空间上的一个完备事件群, 即 , 其和为必然事件, 记 , 则 . 由上面知, 在一次试验中, 事件 必然发生一个且仅发生一个. 现在把该试验独立重复 次, 以 记事件 出现的次数, , 则称 服从多项分布, 记为
其中 , 证明:
(1) 在给定 的条件下服从三项分布 , 其中 , ;
(2) 设 , 则