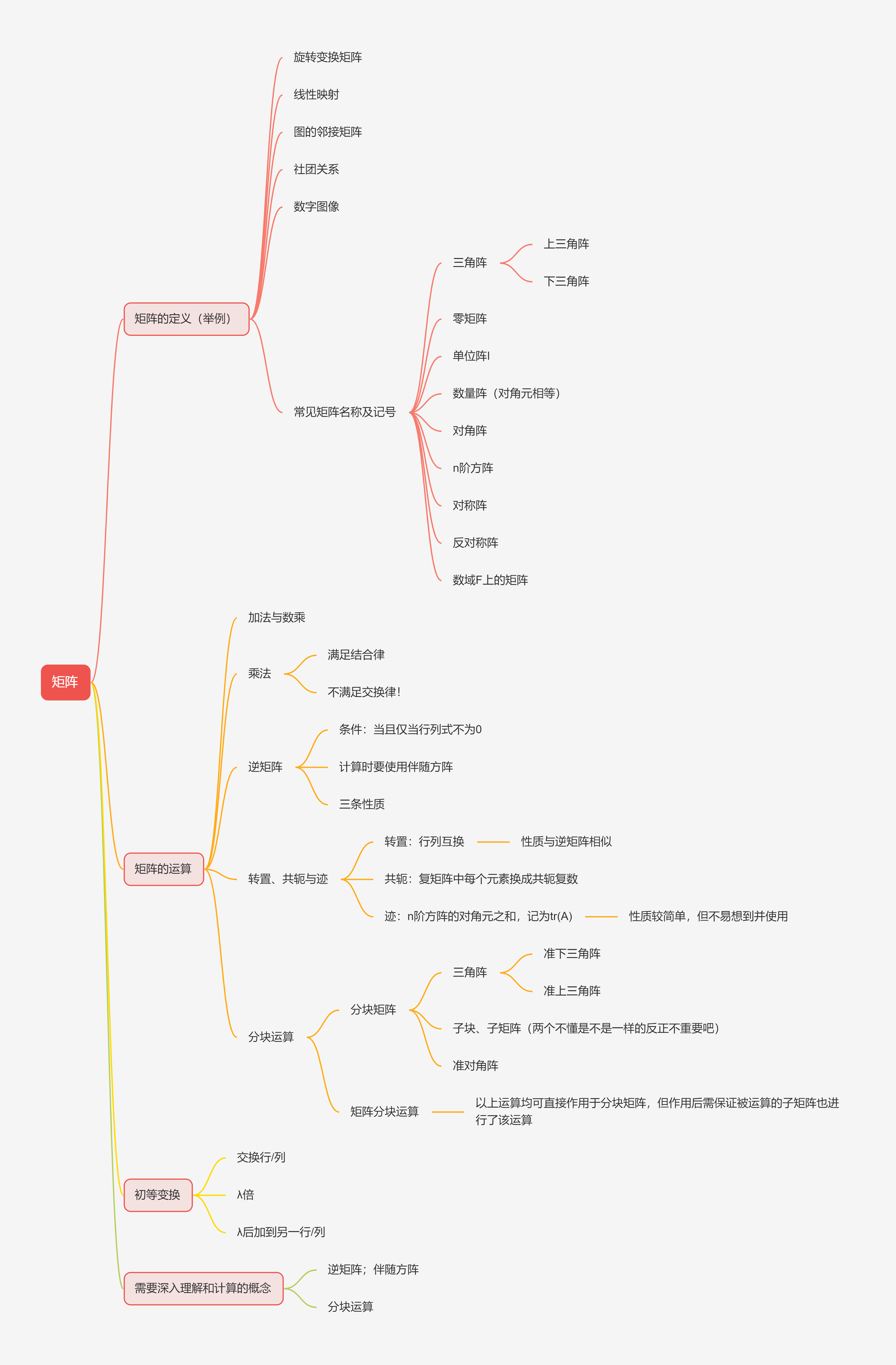
矩阵

📌重点!!!

1. 矩阵乘法的题目
2. 逆矩阵的相关理论
3. 分块运算
4. 初等方阵的性质
5. 分块矩阵的线性变换性质以及关键公式 (和行列式相关的部分)

矩阵运算

矩阵乘法

(2) 即使 $A$ 与 $B$ 是同阶方阵, $A B \text{与} B A$ 也不一定相等. 若 $A B=B A$, 则称 A, B 乘法可交换.

(4) 在 $A$ 的左边乘上对角阵相当于将 $A$ 的各行分别乘上一个数, 在 $A$ 的右边乘上对角阵相当于将 $A$ 的各列分别乘上一个数.

常用矩阵

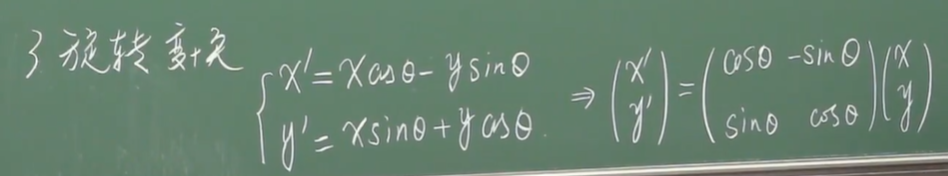
方阵的幂次定义

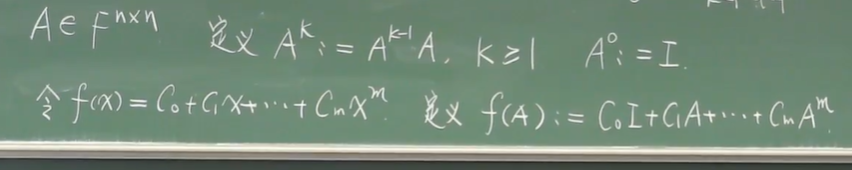
eg1：$A^2=-I$ (充分利用旋转变换的性质 ($\theta$ 是个变量))

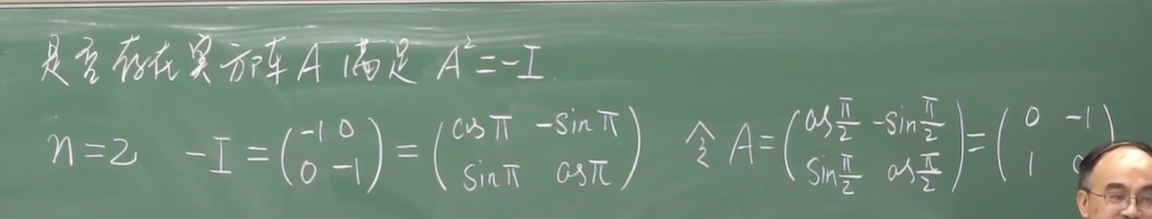
eg2：乘法可交换（阿贝尔群）（可用归纳法证明）

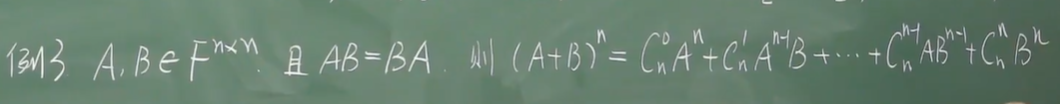
eg3：幂运算时的矩阵加式分解

常用于幂次计算

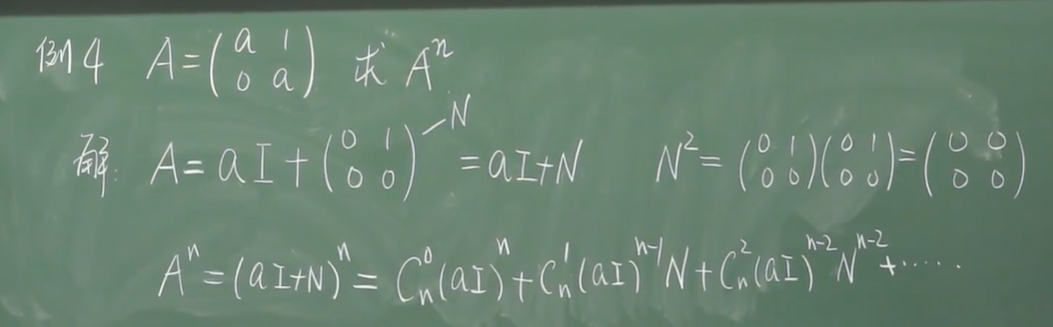
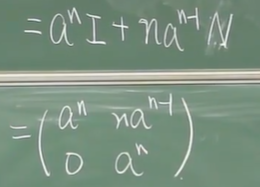
eg4：矩阵乘式分解

重点是第一步的分解

1. 乘法与行列式的定理 $\det(AB)=\det(A) \cdot \det(B)$ (注意此处倘若 AB 不是方阵, 则可将其拓展成方阵, 乘积为 0)

• 几何理解：此处行列式具有了新意义：即面积/体积的变换比例，而这种变换的复合（矩阵相乘）在比例上（行列式）即为乘积

• 证明

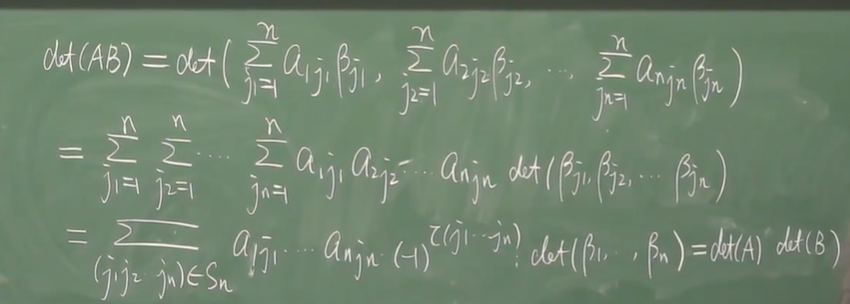
• eg: 矩阵分解算行列式!!!

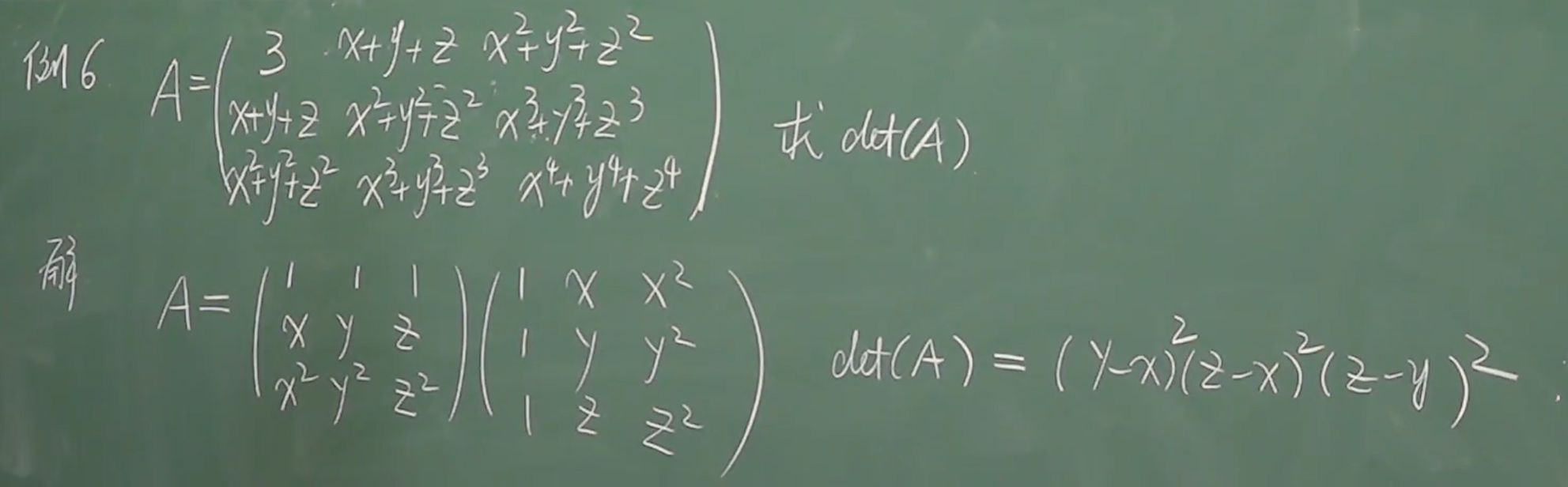
矩阵是线性映射或线性变换, 是线性代数的基础

逆矩阵

定义

设 A 是一个 n 阶方阵, 如果存在 n 阶方阵 X 满足 $X A=A X=I$, 则称 A 可逆, 并称 X 为 A 的逆矩阵, 记作 $A^{-1}$. 可逆方阵也称为非奇异方阵, 称不可逆方阵为奇异方阵.

矩阵逆的其他判定条件

1. det=0
2. r=n
3. 可分解成一系列（有限个）初等方阵的乘积

性质

$(AB)^{-1}=B^{-1}A^{-1}$ $(\lambda A)^{-1}={\lambda}^{-1}A^{-1}$

逆矩阵存在定理

(定理 4.2.4)

设 A 为 n 阶方阵. A 可逆当且仅当 $\operatorname{det}(A) \neq 0$，且

$$\textcolor{red}{A^{-1}=\frac{1}{\operatorname{det}(A)} A^{*}}$$$$\det(A^{-1})=\frac{1}{\det(A)}\qquad \det(A^*)=(\det(A))^{n-1}$$$$\text{注意!!} \textcolor{red}{AA^*=\det A I}\text{恒成立}!!$$$$A^{*}=\left(\begin{array}{cccc}A_{11} & A_{21} & \cdots & A_{n 1} \\\\A_{12} & A_{22} & \cdots & A_{n 2} \\\\\vdots & \vdots & \ddots & \vdots \\\\A_{1 n} & A_{2 n} & \cdots & A_{n n}\\\end{array}\right) \text {, }$$

$A_{i j}$ 是 $a_{i j}$ 的关于行列式 $\operatorname{det}(A)$ 的代数余子式. 称 $A^{*}$ 为 A 的伴随方阵.

注意：伴随方阵的元素是原矩阵对称元素的余子式与代数余子式

eg：二阶与三阶的逆（含向量组表示！）

$(1)\quad \left.ad\neq bc,\quad\left(\begin{array}{cc}a&b\\c&d\end{array}\right.\right)^{-1}=\dfrac{1}{ad-bc}\left(\begin{array}{cc}d&-b\\-c&a\end{array}\right)$

$(2)\quad a,b,c\in F^3,\text{且}a\times b\cdot c\neq0$

$$\left.\left(\begin{array}{c}a\\b\\c\end{array}\right.\right)^{-1}=\frac{1}{a\times b\cdot c}\left(\begin{array}{c}b\times c\\c\times a\\a\times b\end{array}\right)^{T}$$

转置、共轭、迹

转置矩阵性质及简记

定理 4.2.6. 矩阵的转置运算具有以下性质： (1) $(A+B)^{T}=A^{T}+B^{T}$ (2) $(\lambda A)^{T}=\lambda A^{T}$ (3) $(A B)^{T}=B^{T} A^{T}$ (4) $\left (A^{-1}\right)^{T}=\left (A^{T}\right)^{-1}$

其中 $A, B$ 是使运算有意义的矩阵，$\lambda$ 是数。

（1）（2）合并为线性性

（3）转置导致原有的行列发生了倒转，由于矩阵乘法的不可交换性（前行乘后列），必须反向

（4）逆（A*）和转置涉及了行列互换（A*中的代数余子式的下标可见一斑）

矩阵迹的性质（重点为乘式交换顺序迹不变）

$$\begin{aligned} &(1) \operatorname{tr}(A+B)=\operatorname{tr}(A)+\operatorname{tr}(B) \\ &(2) \operatorname{tr}(\lambda A)=\lambda \operatorname{tr}(A) \\ &(3) \operatorname{tr}\left(A^{T}\right)=\operatorname{tr}(A), \ \operatorname{tr}(\bar{A})=\overline{\operatorname{tr}(A)} \\ &(4) \operatorname{tr}(A B)=\operatorname{tr}(B A) \quad \text{（可通过对角元和式表示验证）} \\ \end{aligned}$$

其中 $A, B$ 是使运算有意义的矩阵, $\lambda$ 是数。

• eg：$\operatorname{tr}\left (A \bar{A}^{T}\right)=0\Longleftrightarrow A=O.$（推至实矩阵也可）

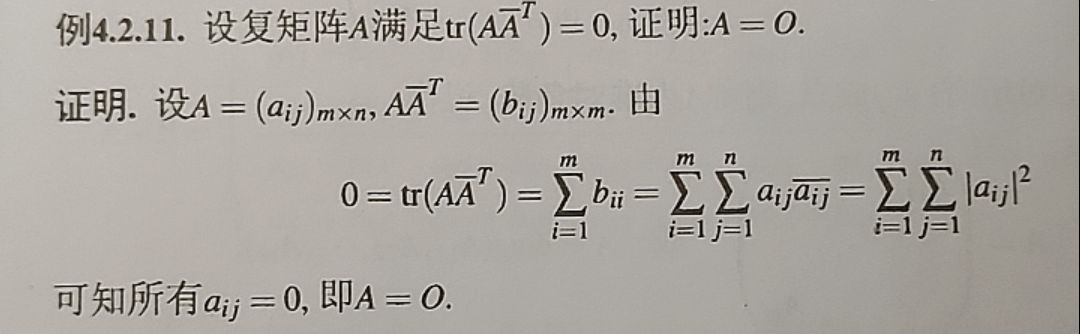
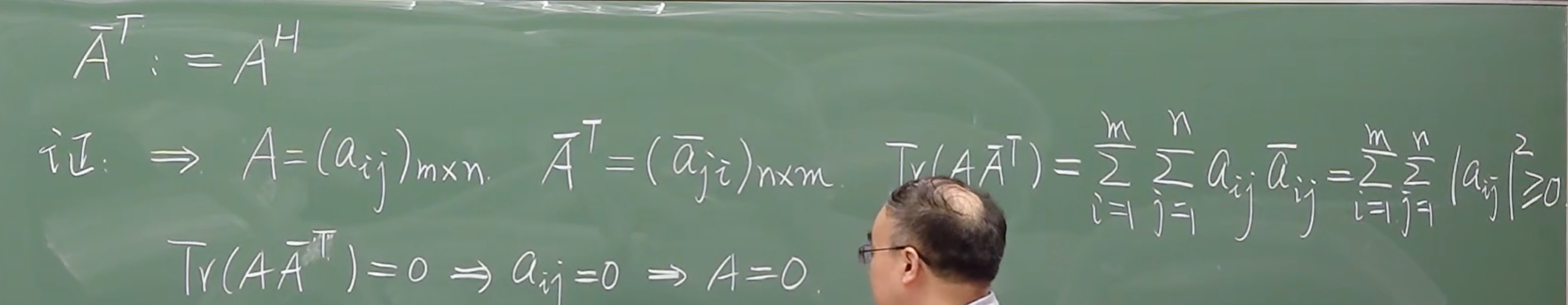
• eg: 性质 1+相似具有相同的迹刷题 (线代)

分块运算

分块矩阵中一定可行的几种变换

在分块方式是运算有意义的情况下：

$$A=\begin{pmatrix}A_1&A_2\\[2ex]A_3&A_4\end{pmatrix},\quad B=\begin{pmatrix}B_1&B_2\\[2ex]B_3&B_4\end{pmatrix}$$$$A+B=\left(\begin{matrix}A_1+B_1&A_2+B_2\\A_3+B_3&A_4+B_4\end{matrix}\right)$$$$AB=\begin{pmatrix}A_1B_1+A_2B_3&A_1B_2+A_2B_4\\A_3B_1+A_4B_2&A_3B_2+A_4B_4\end{pmatrix}$$$$\lambda A=\begin{pmatrix}\lambda A_1&\lambda A_2\\\lambda A_3&\lambda A_4\end{pmatrix},A^T=\begin{pmatrix}A_1^T&A_3^T\\A_2^T&A_4^T\end{pmatrix},\overline{A}=\begin{pmatrix}\overline{A_1}&\overline{A_2}\\\overline{A_3}&\overline{A_4}\end{pmatrix},\:\mathrm{tr}(A)=\mathrm{tr}(A_1)+\mathrm{tr}(A_4)$$

(7) 当 $A_{1}, \cdots, A_{r}$ 都可逆时, $\left (\operatorname{diag}\left (A_{1}, \ldots, A_{r}\right)\right)^{-1}=\operatorname{diag}\left (A_{1}^{-1}, \ldots, A_{r}^{-1}\right).$

行列式*分块

设 A 是 $m \times n$ 矩阵, B 是 $n \times m$ 矩阵。证明：

$$\operatorname{det}(I-B A)=\operatorname{det}\left(\begin{array}{ll}\\I & A \\\\B & I\\\end{array}\right)=\operatorname{det}(I-A B)$$

证. 我们有如下两种分块形式的矩阵乘积分解

$$\begin{aligned}\left(\begin{array}{ll}I & A \\\\B & I\\\end{array}\right) & =\left(\begin{array}{ll}I & O \\\\B & I\\\end{array}\right)\left(\begin{array}{cc}I & O \\\\O & I-B A\\\end{array}\right)\left(\begin{array}{ll}I & A \\\\O & I\\\end{array}\right) \\\\ \left(\begin{array}{ll}I & A \\\\B & I\\\end{array}\right) & =\left(\begin{array}{cc}I & A \\\\O & I\\\end{array}\right)\left(\begin{array}{cc}I-A B & O \\\\O & I\\\end{array}\right)\left(\begin{array}{ll}I & O \\\\B & I\\\end{array}\right)\\\end{aligned}$$

分别计算等式两边方阵的行列式, 即可得证。

伴随矩阵性质

$(0)\quad n=1\text{时，规定}A^* = (1)$

$(1)\quad(\lambda A )^* =\lambda ^{n-1}A^*$

$(2)\quad (AB)^*=B^*A^*$ (用行列式)

$(3)\quad\det(A^*)=(\det(A))^{n-1}$

$(4)\quad A\text{可逆时},(A^{-1})^{*}=(A^{*})^{-1}$

$(5)\quad(A^\mathrm{T})^* = (A^*)^\mathrm{T}$

$(6)\quad AA^* = A^*A = |A|I_n$

伴随矩阵秩

$$\begin{aligned}& \text { rank }(A)=n \Longleftrightarrow \operatorname{rank}\left(A^{*}\right)=n \\& \operatorname{rank}(A)=n-1 \Longleftrightarrow \operatorname{rank}\left(A^{*}\right)=1 \\& \operatorname{rank}(A) \leqslant n-2 \Longleftrightarrow \operatorname{rank}\left(A^{*}\right)=0\end{aligned}$$

• 证明

初等变换

初等方阵具有下列性质:

(1) $S_{i j}$ 为对称方阵, 且 $S_{i j}^{-1}=S_{i j}$（交换位置）;

(2) $D_{i}(\lambda)$ 为对角方阵, 且 $D_{i}(\lambda)^{-1}=D_{i}\left (\lambda^{-1}\right)$（某一行/列倍乘）;

(3) $T_{i j}(\lambda)$ 为三角方阵, 且 $T_{i j}(\lambda)^{-1}=T_{i j}(-\lambda)$（某一行乘 $\lambda$ 加到另一行）.¹

矩阵的秩与相抵

定义：A 可初等变换到 B，则 A 与 B 相抵，记为 $A \sim B$

相抵标准形

相差可逆方阵，秩不变

矩阵的秩等于其非零子式的最高阶数（算秩未必好用，常用初等变换）

与秩有关的问题都使用标准形即可

↑和基联系

LU 分解

应用：求解线性方程组 $AX = \beta$，转化为 $LUX = \beta$。

先求解 $LY = \beta$，得 $Y$；再求解 $UX = Y$，得 $X$。

• eg：LU 分解

这里存在对应关系，可以直接由第一行写出 L 矩阵