线性变换

$F^n$ 上的线性变换

线性映射维度不限

线性变换必须同维

表示方式

$$\varphi_A\colon\quad\mathbb{F}^n\quad\longrightarrow\quad\mathbb{F}^m$$$$L(\mathbb{F}^n,\mathbb{F}^m):\text{线性映射集}$$$$L(\mathbb{F}^n):\text{线性变换集}$$$$\mathcal{A},\mathcal{B}\cdots\in L(\mathbb{F}^n,\:\mathbb{F}^m)$$

给定运算，$\varphi_A$ 唯一

线性变换

恒等变换 $X\longmapsto X$

数乘变换 $X\longmapsto\lambda_{0}X$

伸缩变换 $A=\begin{pmatrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{pmatrix}$, $\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}\longmapsto\begin{pmatrix}\lambda_1x_1\\\lambda_2x_2\\\vdots\\\lambda_nx_n\end{pmatrix}$

同构映射 $A$ 为可逆方阵，$(\varphi_A)^{-1}=\varphi_{(A)^{-1}}$

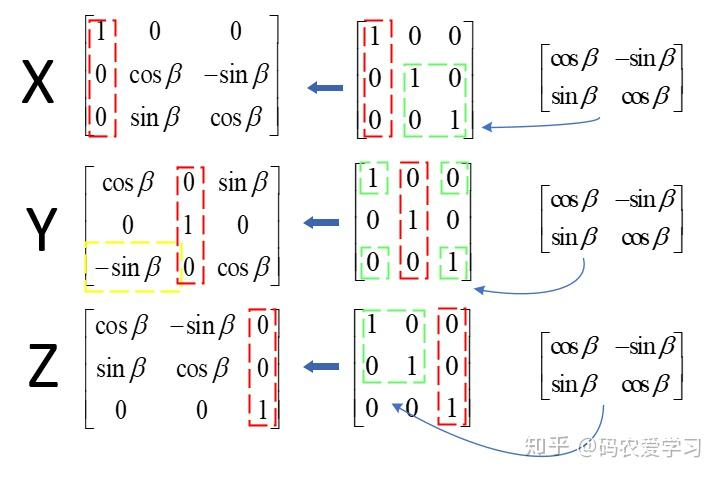
旋转变换，绕原点逆时针转 $\theta$ 角，$\begin{pmatrix}x^{\prime}\\y^{\prime}\end{pmatrix}=\begin{pmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}$

三维旋转，绕哪个轴旋转，就用二维旋转矩阵替换剩下对应的 4 个位置，注意绕 Y 的 -sinβ位置

错切变换，$A=\begin{pmatrix}1&c\\0&1\end{pmatrix}$，c 称为错切因子

线性映射性质

$\mathcal{A}(0)=0$

$\mathcal{A}(-X)=-\mathcal{A}(X)$

$\mathcal{A}(\lambda_1X_1+\cdots+\lambda_sX_s)=\lambda_1\mathcal{A}(X_1)+\cdots+\lambda_s\mathcal{A}(X_s)$

$X_1,\:X_2,\cdots,X_s\text{ 在 }\mathbb{F}^n\text{ 中线性相关}\Rightarrow\mathcal{A}(X_1),\:\mathcal{A}(X_2),\cdots,\mathcal{A}(X_s)\text{ 在 }\mathbb{F}^m\text{ 中线性相关}$

判断变换线性性

$\text{在 }\mathbb{R}^2\text{ 中,}\mathcal{A}(x,\:y)=(x+y,\:x^2)$ 有平方项，不线性

$\text{在 }\mathbb{R}^3\text{ 中,}\mathcal{A}(x,\:y,\:z)=(x-y,\:z,\:x+1)$ ，有不受控的常数项，不线性

$\text{在 }\mathbb{R}^3\text{ 中,}\mathcal{A}(x,\:y,\:z)=(3x-2y+z,\:0,\:x+2y)$ ，由 0 和变量组成，线性

线性变换的复合

$\text{设 }\mathcal{A}\in L(\mathbb{F}^n,\mathbb{F}^m),\mathcal{B}\in L(\mathbb{F}^m,\mathbb{F}^l)\text{,则 }\mathcal{B}\circ\mathcal{A}\in L(\mathbb{F}^n,\mathbb{F}^l)$

等效于矩阵的乘法

线性映射的核与像

考虑 $\mathcal{A}\in L(\mathbb{F}^n,\:\mathbb{F}^m)$

$\begin{aligned}\operatorname{Ker}\mathcal{A}:=\{X\in\mathbb{F}^n\mid\mathcal{A}(X)=0\}\end{aligned}$ (核空间)

$\operatorname{Im}\mathcal{A}:=\{\mathcal{A}(X)\mid X\in\mathbb{F}^n\}$ (像空间)

$\mathcal{A}$ – 映射与核像

$\mathcal{A}\text{ 是单射}\Longleftrightarrow\operatorname{Ker}\mathcal{A}=0$

$\mathcal{A}\text{ 是满射}\Longleftrightarrow\operatorname{Im}\mathcal{A}=\mathbb{F}^m$

$A\text{ 是同构}\Longleftrightarrow\operatorname{Ker}\mathcal{A}=0\And\operatorname{Im}\mathcal{A}=\mathbb{F}^m$

一些解释

联系左乘矩阵 A

$\operatorname{Ker}\mathcal{A}=V_A$

$A=(\alpha_{1}\:\alpha_{2}\:\cdots\:\alpha_{n})\text{,则}\operatorname{Im}\mathcal{A}=<\alpha_{1},\:\alpha_{2},\cdots,\alpha_{n}>$

$\begin{aligned}\dim\text{Ker }\mathcal{A}+\dim\text{Im}\mathcal{A}=n=\dim\mathbb{F}^n\end{aligned}$

特征值与特征向量

特征值可描述矩阵大多数的性质

特征值与特征向量

$AX=\lambda X$，$\lambda\in\mathbb{F},\text{ 非零向量 }X\in\mathbb{F}^n$

$\lambda$ 为特征值，可有多个

X 为 A 的属于 $\lambda$ 的特征向量，一般有无穷多个

已知 X，唯一确定 $\lambda$ ；反之不成立

$V_A (\lambda):=\{X\in\mathbb{F}^n\mid AX=\lambda X\}$，属于 $\lambda$ 的特征子空间

*$V_A$ 是核空间，即 $V_A:=\{X\in\mathbb{F}^n\mid AX=0\}$

特征多项式

$p_A(\lambda)=|\lambda I_n-A|$

求特征值与特征向量

1. 特征多项式的根即为 $\lambda_i$

2. 解出对应的 $X_{i1}, X_{i2},\cdots$（基础解系）

3. $\lambda_i$ 对应的特征向量为 $\begin{aligned}k_{i1}X_{i1}+k_{i2}X_{i2}+\cdots+k_{it_i}X_{it_i}, (\: k_{i1},\: k_{i2},\cdots, k_{it_i}\in\mathbb{F},\text{不全为零 })\end{aligned}$ $V_A(\lambda_i)=\{k_{i1}X_{i1}+k_{i2}X_{i2}+\cdots+k_{it_i}X_{it_i}\mid k_{i1},\cdots,k_{it_i}\in\mathbb{F}\}$

特征值目的

解决幂次运算

$\operatorname{tr}(A)=\sum_{i=1}^n\lambda_i$

$\det(A)=\lambda_1\lambda_2\cdots\lambda_n$

$A\in\mathbb{C}^{n\times n}\text{ 可逆}\Longleftrightarrow A\text{ 的 }n\text{ 个特征值都不为零}$

特征值运算

注意都是 A 和自己运算！！！

$\begin{aligned}&(1)\lambda_0^k\text{ 为 }A^k\text{ 的特征值}.\\&(2)\lambda_0^2-\lambda_0+2\text{ 为 }A^2-A+2I_n\text{ 的特征值}.\\&(3)\text{ 若 }A\text{ 可逆},\text{则 }\frac1{\lambda_0}\text{ 是 }A^{-1}\text{ 的特征值}.\\&(4)\text{ 若 }\lambda_0\neq0,\text{ 则 }\frac1{\lambda_0}\det(A)\text{ 为 }A^*\text{ 的特征值}.\\&(5)\lambda_0\text{ 也是 }A^\mathrm{T}\text{ 的特征值}.\end{aligned}$

矩阵相似

$A\text{ 与 }B\text{ 相似}\overset{def}{\operatorname*{\Longleftrightarrow}}\exists\text{可逆矩阵 }P,\textbf{s.t. }B=P^{-1}AP$

$A\overset{\text{相似}}{\sim}B$

矩阵之间的等价关系的一种

相似性质

$A\overset{\text{相似}}{\sim}B\Rightarrow\begin{cases}(1)\forall\text{ 正整数 }k,A^k\overset{\text{相似}}{\sim}B^k;\\(2)\forall\text{ 多项式 }f(x),f(A)\overset{\text{相似}}{\sim}f(B)\end{cases}$

$A\overset{\text{相似}}{\sim}B\Rightarrow\begin{cases}\text{rank}(A)=\text{rank}(B);\\|A|=|B|;\\\text{tr}(A)=\text{tr}(B);\\p_A(\lambda)=p_B(\lambda).\end{cases}$

以上为相似不变量，不能反推出相似

可对角化条件

A 相似于对角阵

A 有 n 个线性无关的特征向量

A 的不同特征值的特征向量线性无关

n 个不同特征值 → A 相似于对角阵

考虑 $A=P\Lambda P^{-1}$

P 是特征向量排列

$\Lambda$ 是特征值排列