2 随机变量及其分布
一些定义
概率密度函数
表示概率
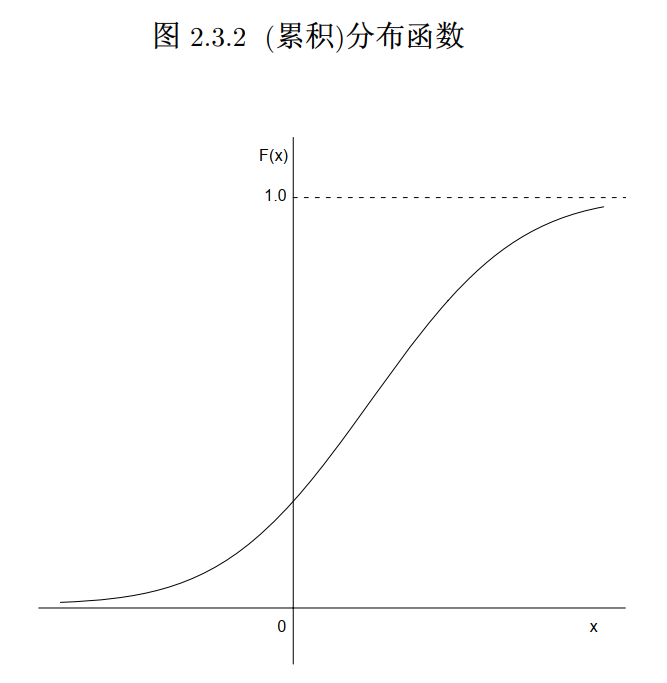
累积分布函数
表示 X 的值≤x 的概率,且
适用于任何随机变量的定义
各种分布
Bernoulli 试验,0-1 分布
设一个随机试验只有两个可能结果 ,则称此试验为 Bernoulli 试验.
1 二项分布
又称 n 重伯努利试验
A 发生的次数为 X, 共试验 n 次
分布函数,以 为例,(0,1)内都可以是中位数
2 Poisson 分布
大概是在均匀分布的样本空间中发现 X 个样本的概率
Poisson 极限定理
n 重 Bernoulli 试验,用 代表 A 在试验中出现的概率,与实验总数 n 有关。如果 → , 则当 时
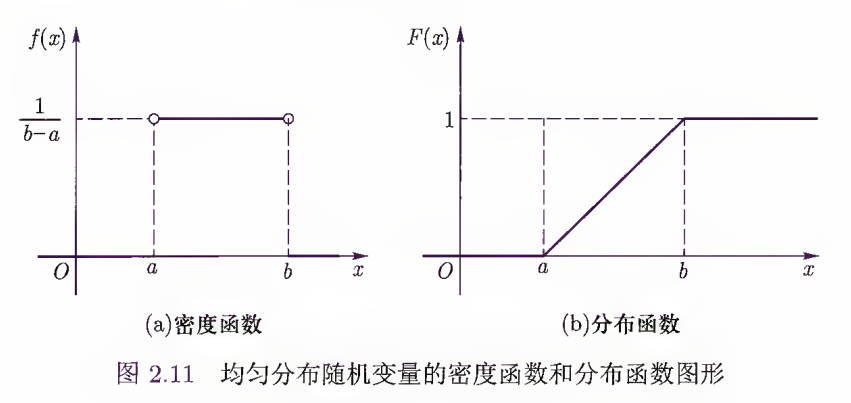
3 均匀分布
, 服从区间 上的均匀分布
4 指数分布
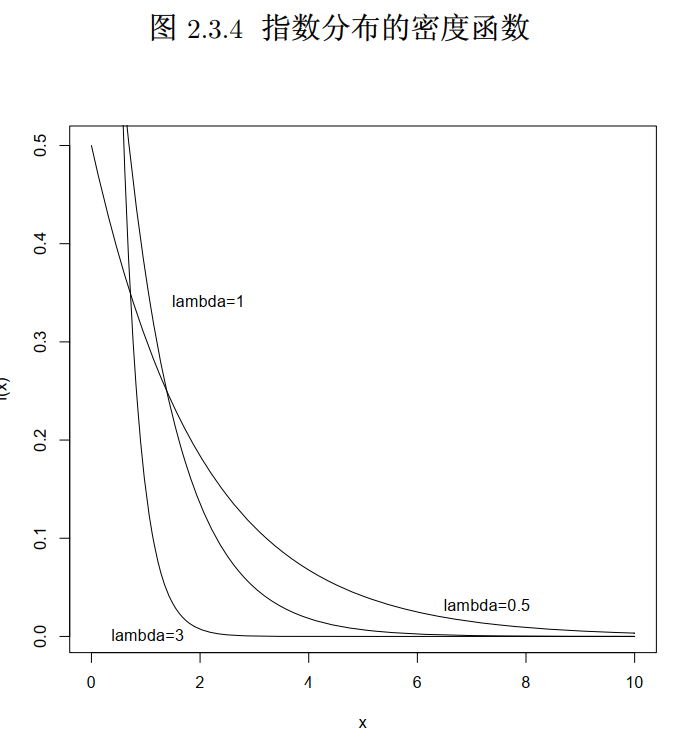
, X 服从参数为 的指数分布
为常数, 越大,密度函数下降得越快 1
无记忆性
证明
注意到
5 正态分布
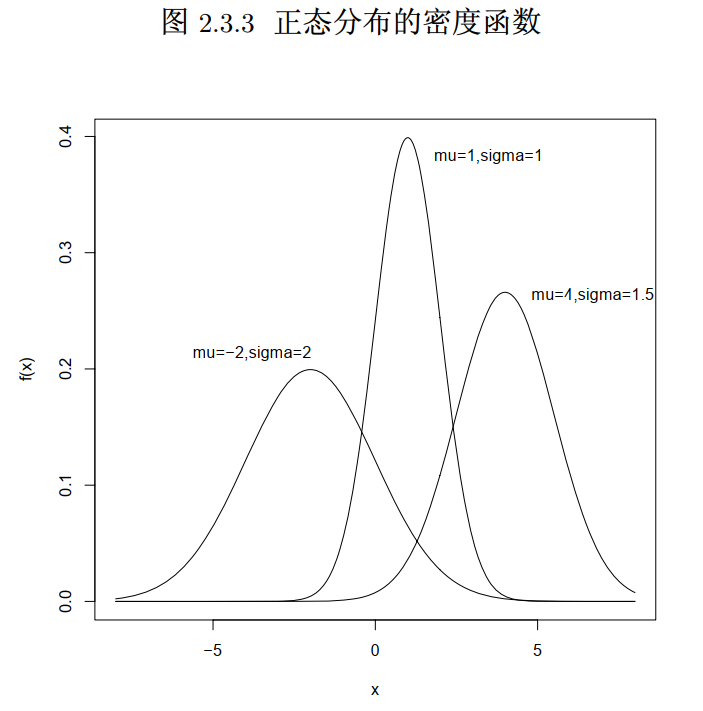
参数为 和 的正态分布
标准正态分布: , , 和 表示标准正态分布 N (0,1) 的分布函数和密度函数
位置参数 :对称轴的位置
形状参数 :越小越陡 2
这部分内容详细见 2_0 多维随机变量及其分布
多维分布(联合分布)
多维随机变量或者随机向量,其中变量之间可能相关可能无关
按照 的类型可分为离散型和连续型
n 维随机变量 的概率函数
其中 可取 ,显然
边缘分布
n 维随机变量中抽出任意 m 维组成变量的分布,为原来联合分布的边缘分布
以二维分布为例,其分布函数为:
边缘分布
条件分布
给定条件下某个变量的分布,比如给定二维分布固定其中一维得到的分布
* 条件分布和边缘分布的区分
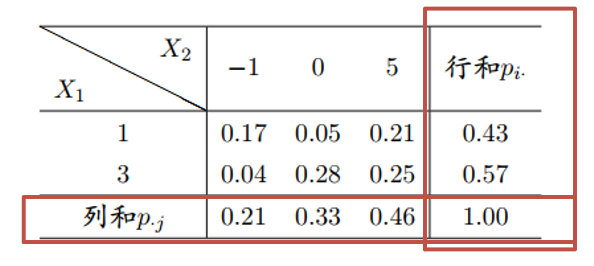
行和或列和是边缘分布
单独的行或列是条件分布